纠错码(Error-correcting codes)
由于电源线的尖峰电压或者其他原因,计算机主存偶尔也会出现错误。这些错误可能导致软件无法正常使用,记录的信息不正确等。当用户频繁遇到这些问题,很可能把计算机砸掉的心都有了。
为防止这些错误,一些主存中采用纠错码,即往每个主存字中按特别的规定加上一些附加位,当从主存中读出一个字时,用这些附加位来检验主存是否出错。
可以类比为如果光盘上出现了轻微的划痕要保证其仍可以被正确地读取内容,就需要用到纠错码去增强其容错性。
不管是文本、图像、音频还是视频,其最终都是被转换成 0 和 1 组成的一串内容被存储在计算机的内存上,比如:
0010011110101000110010000111110101010001110...
最简单的纠错策略就是将这串内容保存三份(甚至更多份),计算机在读取这部分内容时,就可以去比较这三份拷贝,如果三份内容有差别,就以相同的两份为准去修改另一份的内容。
0010011110001000110010000111110101010001110...
0010011110 1 01000110010000111110101010001110...
0010011110 1 01000110010000111110101010001110...
这样一种纠错策略意味着有三分之二的内容都是冗余的,而且即使浪费了这么大的内存空间,也不能可靠地处理多个比特位被同时翻转的情况。
0010011110 1 01000110010000111110101010001110...
0010011110001000110010000111110101010001110...
0010011110001000110010000111110101010001110...
所以我们需要一种方法既可以准确地纠正错误,也可以尽可能少地占用内存空间。
下面我们来设计一个编码系统,它有 m 位数据位,r 位校验位,并能纠正所有一位错。对 2^m 个合法的内存字中的每一个,它的 n 个二进制位中的每一位出错都应是一个非法字,即每个合法码字都对应着 n 个与它码距为 1 的非法码字,它们可以通过将合法码字中的 n 位二进制逐一改变而得到。这样,2^m 个合法码字中的每个都需要有 n+1 个码字与之对应(包括 n 个可能的错误码字和 1 个正确码字)。又因为 n 位编码最多可能有 2^n 个组合,要满足要求,则必须是 (n+1)2^m <= 2^n,将 n = m + r 代入,得到 (m + r + 1) <= 2^r。给定数据位 m 后,就可得到要纠正一位错的最少校验位。
| 字长 | 校验位 | 总长 | 校验位与字长之比(%) |
|---|---|---|---|
| 8 | 4 | 12 | 50 |
| 16 | 5 | 21 | 31 |
| 32 | 6 | 38 | 19 |
| 64 | 7 | 71 | 11 |
| 128 | 8 | 136 | 6 |
| 256 | 9 | 265 | 4 |
| 512 | 10 | 522 | 2 |
接下来,我们看一下海明算法如何对任意字长的内存建立起纠错码。在海明码中,向 m 位数据位上加 r 位校验位,成为 m + r 位字长的新字。这些位从 1 开始计数,最左边的位(最高位)位第 1 位。所有 2 的整数幂的位是校验位,而其他位为数据位。例如:16位字长的字,需加入 5 位校验位,即第1、2、4、8 和 16 位为校验位,其他的都是数据位,存储器的实际字长是 21 位。
| 位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 数据 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
上面表格中空出来的位置即校验位需要填入的数据,现在我们来确定校验位负责校验的位数,一般来说,第 b 位由第 b1、b2、b3、...、bj 位一起来校验,其中 b1+b2+b3+...+bj=b,如下图所示:
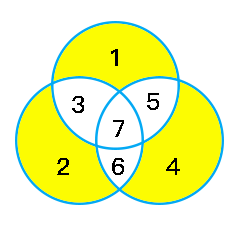
| 位置 | 校验码 | 汇总 |
|---|---|---|
| 1 | 校验位 | |
| 2 | 校验位 | |
| 3 | 1,2 | 1 + 2 = 3 |
| 4 | 校验位 | |
| 5 | 1,4 | 1 + 4 = 5 |
| 6 | 2,4 | 2 + 4 = 6 |
| 7 | 1,2,4 | 1 + 2 + 4 = 7 |
| ... | ... | ... |
因此对于 16 位字长的字来说,每位校验位负责校验的位数分别为:
第 1 位:1、3、5、7、9、11、13、15、17、19、21
第 2 位:2、3、6、7、10、11、14、15、18、19
第 4 位:4、5、6、7、12、13、14、15、20、21
第 8 位:8、9、10、11、12、13、14、15
第 16 位:16、17、18、19、20、21
根据每个校验位负责校验的位数,使用偶校验的方法,填入校验位对应的数据:
| 位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 数据 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
现在我们改变某一位的数据,模拟数据出错的情况:
| 位置 | 1 | 2 | 3 | 4 | 5 |
6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 数据 | 0 | 0 | 1 | 0 | 1 |
1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
假设我们不知道是第 5 位出错了,而是机器自动去判断是否出错以及哪一位出错了,分别检查每个校验位是否满足偶校验,这时候会发现校验位 1 和 4 不满足偶校验,把所有出错的校验位的位号相加就是出错的位号,这里就是第 1+4=5 位出错了,只需把对应第 5 位的数据从 1 改为 0 即可。
如果数据位加校验位的总位数是固定的 2 的整数幂,我们来讨论一下如何确定校验位,以及如何纠一位错。
现在假定数据位加校验位的总位数是 16 位,根据上述的公式 (m + r + 1) <= 2^r,校验位至少需要 4 位,数据位最多为 11 位,剩余的一位可以选择不用或者用于别的用途。
0 1 0 1
0 1 0 1
0 1 0 1
0 1 0 1
这些位从 0 开始计数,校验位的填充位置仍然选取 2 的整数幂位置,除第 0 位之外其他位作为数据位。
0 (1) (0) 1
(0) 1 0 1
(0) 1 0 1
0 1 0 1
第 1 位校验第 2 列和第 4 列的数据,根据偶校验应填入 1;第 2 位校验第 3 列和第 4 列的数据,应填入 0;第 4 位校验第 2 行和第 4 行的数据,应填入 0;第 8 位校验第 3 行和第 4 行的数据,应填入 0。
如果有一个数据位发生了错误,比如第 10 位由 0 变为了 1:
0 (1) (0) 1
(0) 1 0 1
(0) 1 <1> 1
0 1 0 1
根据校验位 1 得知错误不发生在 2、4 列,根据校验位 2 得知错误发生在 3、4列,由此确定错误发生在第 3 列。根据校验位 4 得知校验不发生在 2、4行,根据校验位 8 得知错误发生在 3、4 行,由此确定错误发生在第 3 行。最终确定错误发生在第 3 行第 3 列,将数据从 1 变更为 0 即可将错误修正。
我们将每一位的位号用二进制表示出来。
0000 0001 0010 0011
0100 0101 0110 0111
1000 1001 1010 1011
1100 1101 1110 1111
可以看到第 2 列和第 4 列位号第 4 位都是 1,所以校验位 1 在校验过程中就是在验证错误位置位号第 4 位是不是 1;同理,第 3、4 列第 3 位都是 1,所以校验位 2 验证错误位置位号第 3 位是不是 1;第 2、4 行第 2 位都是 1,所以校验位 4 验证错误位置位号第 2 位是不是 1;第 3、4 行第 1 位都是 1,所以校验位 8 验证错误位置位号第 1 位是不是 1。
还是假设错误发生在第 10 位,我们直接可以得到最终的错误位置二进制位号为 1010,转换为十进制就是 10,这也解释了为什么校验位的位置刚好选择的是 2 的整数幂位置。
由这种方法启发,校验位应该填入的数据可以使用异或运算的方式来确定,我们现在把校验位的数据去掉。
0 ( ) ( ) 1
( ) 1 0 1
( ) 1 0 1
0 1 0 1
然后把所有数据位是 1 的位置的位号一起做异或运算:
0011
0101
0111
1001
1011
1101
1111
------
0001
这样就直接可以确定第一组偶校验组应该再填入一位 1 才能满足偶校验,第二、三
四组校验组则需要填入 0 来满足偶校验。按照顺序在第 1、2、4、8 位填入 1、0、0、0 即可。
0 (1) (0) 1
(0) 1 0 1
(0) 1 0 1
0 1 0 1
0011
0101
0111
1001
1011
1101
1111
(0001)
--------
0000
如果某一位出错了,相当于在异或运算中加上或者去掉了某一位,比如第 10 位由 0 变为了 1:
0011
0101
0111
1001
1011
1101
1111
0001
(1010)
--------
1010
这样我们就直接确定了错误的位置。利用这些简单的思路,我们可以逐渐扩大海明码的应用规模,不过越大规模的存储位可能出错概率更高,只能纠一位错的话就不太适用了,这时候可以考虑更先进的其他纠错码算法。
参考链接:
1.汉明码 Part1 如何克服噪声
2.汉明码 Part2 优雅的全貌
3.计算机组成:结构化方法
